Recently I wrote a review for CS3216. In that post, I briefly touched on the issue of team formation where sub-optimal teams can be formed due to incomplete information and lack of communication. In this post I will explore further on the topic of Game Theory in Project Team Formation, using concepts of Nash Equilibrium and Pareto Optimal. This also serves as a nice example of game theory application in real life.
Scenario Setup
The scenario here is team formation for school projects, where students are allowed to freely pair up with others to form teams and carry out a project on a certain topic. The size of each team has to be exactly 4, with the exception of the last team where the total number of students is not divisible by 4. The topic can be decided among the team members at any time. It can also be changed later as long as it is not too close to the deadline.
The two main variables here are teammates and project topic. We assume that each student has some prior preference for the project topic as well as teammates. We also assume that each students tries his or her best to get the best teammates and project topic from his or her perspective.
Case for Alice and Bob
For simplicity, let’s consider a 2 students, Alice and Bob. Assume that we already have 2 partial teams of 2 formed by 4 other students, the Cat Project (C) and the Dog Project (D), with their project topic already decided. Alice and Bob will only join either C or D, but not any other teams.
For the project topic, Alice prefers C because she likes cat, choosing C will award her a payoff of 2. On the other hand, choosing D only awards her payoff of zero, since she is not terriably against dogs. Bob’s preference for project topic is exactly the opposite, with a payoff of zero for C and payoff of 2 for D.
In terms of teammates, Alice and Bob has no preferences over existing teammates in C and D since they do not know any of them. However, Alice and Bob both dislike each other based on their past experience and observations. Hence, they will both have a payoff of 2 if they are not in the same team, and a payoff of -2 if they are in the same team. Note that the penalty for them being in the same team is higher than that of choosing a project topic that they do not prefer.
Constructing the Payoff Matrix
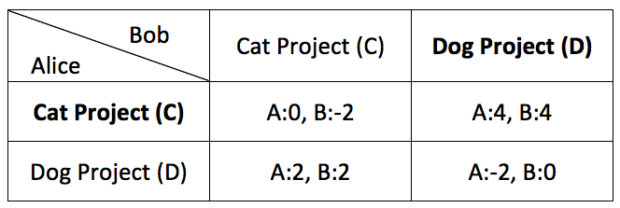
Based on the information above, we can construct the payoff matrix for this scenario:
For instance, consider cell CC where they both join the Cat Project. Alice would have a payoff of 2 (preferred project topic) plus -2 (non-preferred teammates) = 0. Bob would have a payoff of zero (non-preferred project topic) plus -2 (non-preferred teammates) = -2. We do the same calculation for all 4 cells to get the table shown above.
Immediately, we can see that the only Pareto Optimal solution for this case is CD, where Alice choose C and Bob choose D, with a payoff of 4 to both players. This solution dominates all other solutions hence it is the only possible Pareto Optimal solution.
However, in terms of Nash Equilibrium, we have two of them, cell DC (Alice-D, Bob-C) and cell CD(Alice-C, Bob-D). Cell DC is the interesting cell here because it is not Pareto Optimal but it is a Nash Equilibrium. Once both players get into the cell, they would not want to move out. If they move out, they risk decreasing a payoff of 2 given the other player does not move. Hence, there is possibility of attaining this sub-optimal solution instead of the Pareto Optimal solution.
Incomplete Information
All these would not be a problem if they just choose cell CD instead of cell DC. So is cell DC even possible in the first place? The answer is yes.
Unlike what we are doing here with a payoff matrix, Alice and Bob are the players in the real world with incomplete information. They both do not know each other’s preference for the project topic. All they know is their own preference for the project topic and the preference of avoiding each other. This also means they will likely avoid contacts with each other directly, further preventing them from knowing each other’s preferences.
Even though Bob would prefer the Dog Project, he might assume that Alice would naturally also prefer it (when in fact she does not). Because the penalty for being in the same team is higher than not getting the preferred team project, Bob might choose to join the Cat Project instead. And once Alice knows that information (by trying to join the Cat Project and querying the current members), she would join the Dog Project to maximize her payoff, leading to the sub-optimal solution.
There might also be external factors driving the behaviors of Alice and Bob, which may lead to the sub-optimal solution once one player makes a sub-optimal move. Bottomline is, there is a possibility that both players end up with a sub-optimal solution if they do not communicate properly or share information. But if we introduce perfect and publicly available information through a 3rd party, then both players can easily obtain the optimal solution even without communicating directly with each other.
Life is not a zero sum game. We just need to make informed choices.
Concepts on Game Theory mainly from CS4246 AI Planning and Decision Making, check out my CS4246 module review if you are interested.

2 comments